What is a Linearity Property?
Linearity is the property of an element describing a linear relationship between cause and effect. Although the property applies to many circuit elements, we shall limit its applicability to resistors in this chapter. The property is a combination of both the homogeneity (scaling) property and the additivity property. The homogeneity property requires that if the input (also called the excitation) is multiplied by a constant, then the output (also called the response) is multiplied by the same constant. For a resistor, for example, Ohm’s law relates the input i to the output v,
V= iR.
If the current is increased by a constant k, then the voltage increases correspondingly by k, that is,
The additivity property requires that the response to a sum of inputs is the sum of the responses to each input applied separately. Using the voltage-current relationship of a resistor, if
kiR = kV
V1 = i1R
and
V2 = i2R
then applying (i1+i2) gives,
V = (i1+i2)R = i1R + i2R = V1 + V2
We say that a resistor is a linear element because the voltage-current relationship satisfies both the homogeneity and the additivity properties.
In general, a circuit is linear if it is both additive and homogeneous. A linear circuit consists of only linear elements, linear dependent sources, and independent sources.
A Linear Circuit is one whose output is linearly related (or directly proportional) to its input.
Example:
What is a Source Transformation?
We have noticed that series-parallel combination and wye-delta transfor-mation help simplify circuits. Source transformation is another tool for simplifying circuits. Basic to these tools is the concept of equivalence.
We recall that an equivalent circuit is one whose v-i characteristics areidentical with the original circuit.
Before, we saw that node-voltage (or mesh-current) equa- tions can be obtained by mere inspection of a circuit when the sources are all independent current (or all independent voltage) sources. It is therefore expedient in circuit analysis to be able to substitute a voltage source in series with a resistor for a current source in parallel with a resistor, or vice versa. Either substitution is known as a source transformation.
Figure 1:
A Source Transformation is the process of replacing a voltage source Vs in series with a resistor R by a current source Is in parallel with a resistor R, or vice versa.
Source transformation requires that,
Vs = IsR or Is = Vs/R
Source transformation also applies to dependent sources, provided we carefully handle the dependent variable. As shown in below, a dependent voltage source in series with a resistor can be transformed to a dependent current source in parallel with the resistor or vice versa.
Figure 2:
Like the wye-delta transformation we studied in Chapter 2, a source transformation does not affect the remaining part of the circuit. When applicable, source transformation is a powerful tool that allows circuit manipulations to ease circuit analysis. However, we should keep the following points in mind when dealing with source transformation.
- Note from Fig.1 (or Fig.2) that the arrow of the current source is directed toward the positive terminal of the voltage source.
- Note that source transformation is not possible when R=0, which is the case with an ideal voltage source. However, for a practical, nonideal voltage source, R=0. Similarly, an ideal current source with R=∞ cannot be replaced by a finite voltage source.
Example:
Some Learnings:
- Linearity Property talks about the voltage (v) and current (i), whereas voltage is directly proportional to the current, that is, when the voltage is increasing the current also increasing and vice versa.
- Source Transformation is only applicable to simple circuits like the figures below:
- Source Transformation can be applied if and only if the voltage is in series with the resistor and/or the current is in parallel with the resistor.
- In Source Transformation when the polarity of the voltage source has a positive on top therefore the resulting current source is pointing upward and vice versa. Also when the voltage source is dependent therefore the resulting current is also dependent, same goes with independent sources.
For more information, watch the videos below:
For Linearity Property:
For Source Transformation:
That's all. Thank You for visiting my blog.
GOD Bless! :)
By:
AYALA, ARNY S. BSECE -3
ECE 311
Professor:
ENGR. JAY S. VILLAN, MEP - EE

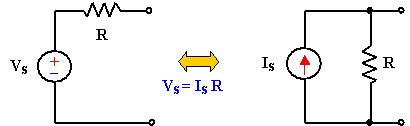








No comments:
Post a Comment